Download the commented source code.
Bézier curves are extremely useful in computer graphics and are hence supported by the iOS Foundation Framework via the UIBezierPath class. Unfortunately, this class is designed for drawing, so it lacks an inbuilt method that allows you to easily interpolate the path, making it very difficult to find the positions and tangents of points along the path. So let's create our own class to do all the interesting cubic Bézier curve calculations unavailable in UIBezierPath.
Create a new class called PWBezier and open the header file.
@interface PWBezier : NSObject
{
// cubic bezier control points
CGPoint _C0, _C1, _C2, _C3;
// cubic polynomial coefficients, such that B(t) = A*t^3 + B*t^2 + C*t + D
CGPoint _A, _B, _C, _D;
}
@property(readonly) CGPoint C0, C1, C2, C3;
@property(readonly) CGPoint A, B, C, D;
We need to store the four control points that define our standard cubic Bézier curve. It's worth remembering that a cubic Bézier curve is really just a cubic polynomial in it's parametric form where:
Bez(t) = At³ + Bt² + Ct + D, for 0 ≤ t ≤ 1
= ((At + B)t + C)t + D
The factorised form of the polynomial is the fastest to compute, so we will also store the cubic polynomial coefficients.
Open the .m file and add the following.
@synthesize C0 = _C0, C1 = _C1, C2 = _C2, C3 = _C3;
@synthesize A = _A, B = _B, C = _C, D = _D;
- (id)initWithOrigin:(CGPoint)C0 controlPoint1:(CGPoint)C1 controlPoint2:(CGPoint)C2 destination:(CGPoint)C3 {
self = [super init];
if (self) {
_C0 = C0;
_C1 = C1;
_C2 = C2;
_C3 = C3;
[self calculateCubicCoefficients];
}
return self;
}
Our first initialiser is very basic - you just supply the origin (start point), control points and destination (end point) and set the instance variables accordingly. Next we need to calculate the cubic coefficients of the polynomial.
- (void)calculateCubicCoefficients {
_A.x = _C3.x - 3.0*_C2.x + 3.0*_C1.x - _C0.x;
_A.y = _C3.y - 3.0*_C2.y + 3.0*_C1.y - _C0.y;
_B.x = 3.0*_C2.x - 6.0*_C1.x + 3.0*_C0.x;
_B.y = 3.0*_C2.y - 6.0*_C1.y + 3.0*_C0.y;
_C.x = 3.0*_C1.x - 3.0*_C0.x;
_C.y = 3.0*_C1.y - 3.0*_C0.y;
_D = _C0;
}
You can take a look at the maths behind the derivation if interested. Evaluating the output is easy and fast using our stored coefficients.
- (CGFloat)outputXAtT:(CGFloat)t {
return ((_A.x*t+_B.x)*t+_C.x)*t+_D.x;
}
- (CGFloat)outputYAtT:(CGFloat)t {
return ((_A.y*t+_B.y)*t+_C.y)*t+_D.y;
}
- (CGPoint)outputAtT:(CGFloat)t {
return CGPointMake(((_A.x*t+_B.x)*t+_C.x)*t+_D.x, ((_A.y*t+_B.y)*t+_C.y)*t+_D.y);
}
We can use these methods to evaluate the x and/or y position of the Bézier curve for any t value, remembering that the start of the curve is at t = 0 and the end of the curve is at t = 1.
To calculate the tangent angle of the curve, we just need the derivative of the polynomial with respect to t.
Bez(t) = At³ + Bt² + Ct + D, for 0 ≤ t ≤ 1
d/dt Bez(t) = 3At² + 2Bt + C
- (CGFloat)tangentAngleAtT:(CGFloat)t {
CGFloat dxdt = 3.0*_A.x*t*t + 2.0*_B.x*t + _C.x;
CGFloat dydt = 3.0*_A.y*t*t + 2.0*_B.y*t + _C.y;
return atan2(dydt, dxdt);
}
In order to draw the curve, we need a UIBezierPath representation.
- (void)addToBezierPath:(UIBezierPath*)bezierPath {
[bezierPath moveToPoint:_C0];
[bezierPath addCurveToPoint:_C3 controlPoint1:_C1 controlPoint2:_C2];
}
- (UIBezierPath*)bezierPath {
UIBezierPath * bezierPath = [UIBezierPath bezierPath];
[self addToBezierPath:bezierPath];
return bezierPath;
}
We can use addToBezierPath: to add the PWBezier to an existing UIBezierPath instance, or use bezierPath to create a new one.
Let's draw our curve and add some perpendicular lines to it. Firstly create a UIView subclass called something like BLBezierView and add a single PWBezier instance variable to the interface.
@class PWBezier;
@interface BLBezierView : UIView
{
PWBezier * _bezier;
}
@end
Initialise the PWBezier instance variable with some arbitrary values in the default UIView initialiser.
- (id)initWithFrame:(CGRect)frame {
self = [super initWithFrame:frame];
if (self) {
[self setBackgroundColor:[UIColor whiteColor]];
_bezier = [[PWBezier alloc] initWithOrigin:CGPointMake(40.0, 200.0)
controlPoint1:CGPointMake(135.0, 100.0)
controlPoint2:CGPointMake(130.0, 280.0)
destination:CGPointMake(280.0, 200.0)];
}
return self;
}
Custom drawing in a UIView is performed by overwriting the drawRect: method. We will start out by getting the UIBezierPath representation of our curve and drawing it by calling it's inbuilt stroke method..
- (void)drawRect:(CGRect)rect
{
UIBezierPath * bezierPath = [_bezier bezierPath];
[[UIColor lightGrayColor] setStroke];
[bezierPath setLineWidth:10.0];
[bezierPath setLineCapStyle:kCGLineCapRound];
[bezierPath stroke];
...
}
Still in the drawRect method, let's iterate along the curve to create perpendicular lines at regular intervals.
- (void)drawRect:(CGRect)rect
{
...
// setup the graphics context
CGContextRef context = UIGraphicsGetCurrentContext();
CGContextSetStrokeColorWithColor(context, [UIColor blueColor].CGColor);
CGContextSetLineWidth(context, 1.0);
NSUInteger divisions = 8;
CGFloat radius = 5.0;
CGFloat lineRadius = 15.0;
CGPoint bezierPoint, normalPoint1, normalPoint2;
CGFloat t, angle;
for(NSUInteger d = 0; d<=divisions; ++d) {
// 0 <= t <= 1
t = ((CGFloat)d)/divisions;
bezierPoint = [_bezier outputAtT:t];
angle = [_bezier tangentAngleAtT:t];
// create a circle at the bezier point
CGRect rect = CGRectMake(bezierPoint.x-radius, bezierPoint.y-radius, 2.0*radius, 2.0*radius);
CGContextAddEllipseInRect(context, rect);
// calculate the normal points which are +/- 90 degrees from the tangent angle
normalPoint1.x = bezierPoint.x + lineRadius*cos(angle + M_PI_2);
normalPoint1.y = bezierPoint.y + lineRadius*sin(angle + M_PI_2);
normalPoint2.x = bezierPoint.x + lineRadius*cos(angle - M_PI_2);
normalPoint2.y = bezierPoint.y + lineRadius*sin(angle - M_PI_2);
// create the perpendicular line
CGContextMoveToPoint(context, normalPoint1.x, normalPoint1.y);
CGContextAddLineToPoint(context, normalPoint2.x, normalPoint2.y);
}
// draw the context
CGContextStrokePath(context);
}
Firstly we setup the graphics context and set the number of divisions. We initialise the loop variable d to 0, and increment it by 1 up to and including the number of divisions. We calculate the current Bézier t value by dividing d by it's maximum value, which ensures 0 ≤ t ≤ 1. Note that we must typecast d to a float to ensure the division result is a decimal number, since integer division will only return whole numbers. The position of the point along the curve can now be calculated, along with the tangent angle.
We can draw a circle around the point by adding an ellipse in a rect with a centre on the curve and a width/height equal to the desired radius. The endpoints of the line perpendicular to the curve are located at an angle of +/- 90 degrees (+/- π/2 radians) from the tangent angle.
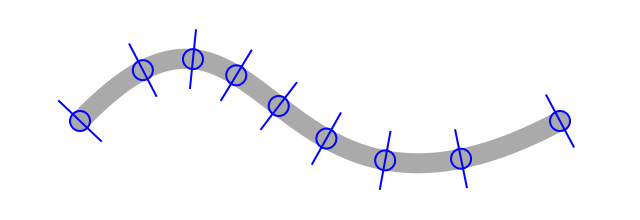
Here is the result.
Great, we can now determine the position and angle of points along a Bézier curve!
Our new PWBezier class is very basic at the moment so we should add some more functionality. Let's make it easier to create a straight line segment.
- (id)initWithStartPoint:(CGPoint)startPoint endPoint:(CGPoint)endPoint {
self = [super init];
if (self) {
_C0 = startPoint;
_C1.x = startPoint.x + 1.0/3.0*(endPoint.x - startPoint.x);
_C1.y = startPoint.y + 1.0/3.0*(endPoint.y - startPoint.y);
_C2.x = startPoint.x + 2.0/3.0*(endPoint.x - startPoint.x);
_C2.y = startPoint.y + 2.0/3.0*(endPoint.y - startPoint.y);
_C3 = endPoint;
[self calculateCubicCoefficients];
}
return self;
}
The control points should be spread out evenly, so we set C0 to the start point of the line, C1 to ⅓ of the way along the line, C2 to ⅔ of the way along the line and C3 to the end point of the line.
Sometimes you'll find it more useful to define a Bézier curve by the points that the curve should intersect with, instead of the control points. You can calculate the cubic Bézier curve that passes through four given points like this:
- (id)initWithStartPoint:(CGPoint)point0 firstMidPoint:(CGPoint)point1 secondMidPoint:(CGPoint)point2 endPoint:(CGPoint)point3 {
self = [super init];
if (self) {
CGPoint pointC, pointD;
pointC.x = point1.x - (8.0*point0.x + point3.x)/27.0;
pointC.y = point1.y - (8.0*point0.y + point3.y)/27.0;
pointD.x = point2.x - (point0.x + 8.0*point3.x)/27.0;
pointD.y = point2.y - (point0.y + 8.0*point3.y)/27.0;
_C0 = point0;
_C1.x = 3.0*pointC.x - 1.5*pointD.x;
_C1.y = 3.0*pointC.y - 1.5*pointD.y;
_C2.x = 3.0*pointD.x - 1.5*pointC.x;
_C2.y = 3.0*pointD.y - 1.5*pointC.y;
_C3 = point3;
[self calculateCubicCoefficients];
}
return self;
}